Conexitate
Lant
Definitie: Fie G=(V, U) un graf orientat. Se numeşte lant, în graful G, o succesiune de arce, notată
L=[ui1 ,ui2 ,...,uik] cu proprietatea ca oricare două arce consecutive au o extremitate comună (nu are importantă orientarea arcelor).
Se întâlnesc notiunile:
- extremitătile lantului
• fiind dat lantul L=[ui1 ,ui2 ,...,uik] se numesc extremităti ale sale extremitatea arcului ui1 care nu este
comună cu arcul ui2 şi extremitatea arcului uik care nu este comună cu arcul uik-1
- lungimea lantului
• fiind dat lantul L=[ui1 ,ui2 ,...,uik] prin lungimea sa se întelege numărul de arce care apar în L;
• Exemplu de lant:
cu reprezentarea grafică astfel:
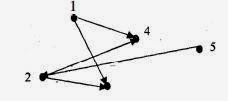
Fie graful G=(V, U), unde: V={1,2,3,4,5}
U={(1,3),(1,4), (2,3), (2,4), (5,2)}= { u1, u2, u3, u4, u5 }
L1=[ u1 ,u3 ,u5] este, în graful G, lanŃ cu lungimea 3 şi extremităŃile 1 şi 5.
L2=[ u1 ,u2, u4, u5] este, în graful G, lanŃ cu lungimea 4 şi extremităŃile 3 şi 5.
Atentie! Dacă L=[ui1 ,ui2 ,...,uik] este lant în graful G, atunci şi L=[uik ,uk-1 ,...,ui1]
este lant în graful G.
Drum
Definitie: Fie G=(V, U) un graf orientat. Se numeşte drum, în graful G, o succesiune de noduri, notată D=(xi1 ,xi2 ,...,xik), cu proprietatea (xi1 ,xi2),..., (xik-1 ,xik) ∈ U(altfel spus (xi1 ,xi2),..., (xik-1 ,xik) sunt arce).
Se întâlnesc notiunile:
- extremitătile drumului
• fiind dat drumul D=(xi1 ,xi2 ,...,xik) se numesc extremităti ale sale nodurile xi1 şi xik (xi1 extremitate initială şi xik extremitate finală) - lungimea drumului
• fiind dat drumul D=(xi1 ,xi2 ,...,xik) , prin lungimea sa se întelege numărul de arce care apar în cadrul său; • Exemplu de drum:
Fie graful G=(V, U) unde:
V={ 1,2,3,4,5 }
U={(1,3), (4,1), (3,2), (2,4), (5,2)}
cu reprezentarea grafică astfel:
D1=(1, 3, 2) este, în graful G, drum cu lungimea 2 şi extremitătile 1 şi 2.
D2=(4, 1, 3, 2) este, în graful G, drum cu lungimea 3 şi extremitătile 4 şi 2
Atentie! Dacă D=(xi1 ,xi2 ,...,xik) este drum, în graful G, atunci nu neapărat şi D1=(xik ,xik-1 ,xi) este drum, în graful G.
Definitie: Fie G=(V,U) un graf orientat. Se numeşte drum elementar, în graful G, drumul
D=(xi1 ,xi2 ,...,xik) cu proprietatea că oricare două noduri ale sale sunt distincte (altfel spus, printr-un nod nu se trece decât o singură dată).
• Exemplu: în graful de mai jos,
drumul D1=(4, 1, 3, 2) este drum elementar.
Definitie: Fie G=(V, U) un graf orientat: Se numeşte drum neelementar, în graful G, drumul
D=(xi1 ,xi2 ,...,xik) cu proprietatea că nodurile sale nu sunt distincte două câte două (altfel spus, prin anumite noduri s-a trecut de mai multe ori).
•
Exemplu: în graful de mai jos,
drumul D2=(4, 1, 3, 2, 4, 5, 2) este drum neelementar (prin 4 (şi 2)
s-a trecut de două ori).
Definitie Un drum hamiltonian într-un graf orientat este un drum care conţine toate vârfurile grafului.
Circuit
Definitie: Fie G=(V, I) un graf neorientat. Se numeşte circuit, în graful G, drumul D=(xi1 ,xi2 ,...,xik)
cu proprietatea că xi1 = xik şi are arcele cel compun diferite două câte două (circuitul se notează în continuare cu C).
• Exemplu: în graful de mai jos,
drumul C=(1, 3, 2, 4, 1) este circuit.
Definitie: Fie G=(V, U) un graf orientat. Se numeşte circuit elementar, în graful G, un circuit cu proprietatea că oricare două noduri ale sale, cu exceptia primului şi a ultimului, sunt distincte.
• Exemplu: în graful de mai jos,
circuitul C=(1, 3, 2, 4, 1) este circuit elementar.
Definitie: Fie G=(V, U) un graf orientat. Se numeşte circuit neelementar, în graful G, un circuit cu
proprietatea că nodurile sale, cu exceptia primului şi a ultimului, nu sunt distincte.
• Exemplu: în graful de mai jos
circuitul C=(1, 3, 4, 2, 5, 4, 1) este circuit neelementar (prin 4 s-a trecut de două ori).
Definitie : Intr-un graf orientat G=(X,U) se numeşte circuit hamiltonian un circuit elementar care conţine toate vârfurile grafului.
Definitie: Intr-un graf orientat G=(X,U) se numeşte circuit eulerian un circuit care conţine toate
arcele grafului.
Definitie: Se numeşte graf eulerian un graf care conţine un circuit eulerian.
Graf conex
Definitie: Fie G=(V, U) un graf orientat. Graful G se numeşte conex dacă pentru oricare două vârfuri x şi y, x#y, există un lant de extremităti x şi y.
• Exemplu de graf care este conex:
Graful este conex, deoarece oricare ar fi vârfurile x şi y, x#y, există un lant in G care să le lege.
• Exemplu de graf care nu este conex:
Graful nu este conex, deoarece există două vârfuri, cum ar fi 1 şi 4, pentru care nu există nici un lant în graf
care să le lege.
Definitie: Un graf este tare conex dacă pentru oricare două vârfuri x, y X există un drum de la x la y şi un drum de la y la x.
Exemplu:
-Graf tare conex

Componentă conexă
Definitie: Fie G=(V, U) un graf orientat. Se numeşte componentă conexă un graf orientat G1=(V1 ,U1) care verifică următoarele conditii:
- este subgraf al grafului G;
- este conex;
- nu există nici un lant în G care să lege un nod din V, cu an nod din V-V1.
• Exemplu: Fie graful G=(V, U) : V={1,2,3,4,5} şi U={(1,2), (3,1), (3,2), (4,5)}
Pentru graful de mai sus, graful G1=(V1,U1) unde: V1={4,5} şi U1={(4,5)} este componentă conexă,
deoarece:
- este subgraf al grafului G;
- este conex;
- nu există nici un lant în G care să lege un nod din V, cu un nod din V-V1={1,2,3}
La fel, se poate spune şi despre graful G2=(V2,U2) unde: V2={1,2,3) şi U2={(1,2)> (3,1), (3,2)}
În concluzie, graful din figura de mai sus este format din două componente conexe.
Observatie: Fie G=(V, U) un graf orientat. Graful G este conex dacă şi numai dacă este format dintr-o
singură componentă conexă.
• Exemplu de graf conex (este format dintr-o singură componentă conexă):
Definitie: O componentă tare conexă a unui graf orientat G=(X, U) este un subgraf G1=(X1,Y1) al lui G care este tare conex şi care este maximal în raport cu această proprietate (adică oricare ar fi x X\X1,
subgraful lui G generat de X1{x} nu mai este tare conex).
Exemplu:
-Graf cu doua componente tare conexe